Numpy Dot

Numpy Dot

NumPy is a fundamental package for scientific computing with Python. Among its many features, the dot function is one of the most versatile and widely used. This article will explore the dot function in NumPy, covering its purpose, usage, and providing numerous examples to demonstrate its capabilities. Each example will include detailed explanations to ensure a thorough understanding of the function.

Introduction to Numpy Dot

The dot function in NumPy computes the dot product of two arrays. For 1-D arrays, it is the inner product of the vectors. For 2-D arrays, it is equivalent to matrix multiplication. For N-D arrays, it is a sum product over the last axis of the first array and the second-to-last of the second array.

import numpy as np

The numpy.dot function can be used for a variety of operations including vector dot products, matrix multiplication, and more complex tensor operations. Let’s explore these in detail.

Basic Usage of Numpy Dot

The most basic usage of the dot function is with 1-D arrays (vectors). When dealing with vectors, the dot product is the sum of the products of the corresponding elements.

Example 1: Basic Dot Product

import numpy as np

# Define two vectors
vector_a = np.array([1, 2, 3])
vector_b = np.array([4, 5, 6])

# Compute the dot product
dot_product = np.dot(vector_a, vector_b)

print(f"Dot product of vector_a and vector_b: {dot_product}")  # numpyarray.com

Output:

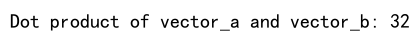
In this example, the dot product of vector_a and vector_b is computed. The operation is straightforward: $(14) + (25) + (3*6) = 32$.

Dot Product of Vectors

The dot product of vectors is a fundamental operation in many scientific and engineering applications. It is used in physics to compute work done by a force, in machine learning for calculating similarities between data points, and much more.

Example 2: Dot Product with Different Lengths

import numpy as np

# Define two vectors of different lengths
vector_a = np.array([1, 2])
vector_b = np.array([3, 4, 5])

try:
    # Attempt to compute the dot product
    dot_product = np.dot(vector_a, vector_b)
    print(f"Dot product of vector_a and vector_b: {dot_product}")  # numpyarray.com
except ValueError as e:
    print(f"Error: {e}")  # numpyarray.com

Output:

This example demonstrates that attempting to compute the dot product of vectors of different lengths results in an error. The dot product requires vectors of the same length.

Example 3: Higher-Dimensional Dot Product

import numpy as np

# Define two higher-dimensional arrays
array_a = np.array([[1, 2], [3, 4]])
array_b = np.array([[5, 6], [7, 8]])

# Compute the dot product
dot_product = np.dot(array_a, array_b)

print(f"Dot product of array_a and array_b:\n{dot_product}")  # numpyarray.com

Output:

In this example, array_a and array_b are 2-D arrays (matrices). The dot function performs matrix multiplication, which involves taking the sum of the products of corresponding elements.

Matrix Multiplication

Matrix multiplication is one of the most common uses of the dot function. It is used in linear algebra, computer graphics, and many other fields.

Example 4: Matrix Multiplication with Different Sizes

import numpy as np

# Define two matrices
matrix_a = np.array([[1, 2, 3], [4, 5, 6]])
matrix_b = np.array([[7, 8], [9, 10], [11, 12]])

# Compute the matrix multiplication
matrix_product = np.dot(matrix_a, matrix_b)

print(f"Matrix product of matrix_a and matrix_b:\n{matrix_product}")  # numpyarray.com

Output:

In this example, matrix_a is a 2×3 matrix, and matrix_b is a 3×2 matrix. The result of their multiplication is a 2×2 matrix. The dimensions of the matrices must align appropriately for the multiplication to be valid.

Example 5: Matrix Multiplication Resulting in Scalar

import numpy as np

# Define two 1x1 matrices
matrix_a = np.array([[2]])
matrix_b = np.array([[3]])

# Compute the matrix multiplication
matrix_product = np.dot(matrix_a, matrix_b)

print(f"Matrix product of matrix_a and matrix_b:\n{matrix_product}")  # numpyarray.com

Output:

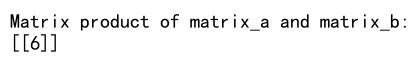
Here, both matrix_a and matrix_b are 1×1 matrices. The result is a single scalar value, which is the product of the two elements.

Dot Product with Scalars

While the dot function is typically used with arrays, it can also handle scalar values. When one of the inputs is a scalar, the function effectively scales the other input by that scalar.

Example 6: Dot Product with a Scalar and a Vector

import numpy as np

# Define a vector and a scalar
vector = np.array([1, 2, 3])
scalar = 4

# Compute the dot product
dot_product = np.dot(vector, scalar)

print(f"Dot product of vector and scalar: {dot_product}")  # numpyarray.com

Output:

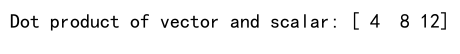
In this example, the vector is scaled by the scalar value. Each element of the vector is multiplied by the scalar, resulting in a new vector.

Example 7: Dot Product with a Scalar and a Matrix

import numpy as np

# Define a matrix and a scalar
matrix = np.array([[1, 2], [3, 4]])
scalar = 5

# Compute the dot product
dot_product = np.dot(matrix, scalar)

print(f"Dot product of matrix and scalar:\n{dot_product}")  # numpyarray.com

Output:

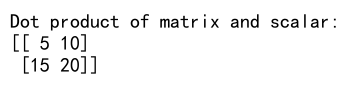
Similar to the previous example, each element of the matrix is scaled by the scalar. The resulting matrix has each element multiplied by the scalar.

Broadcasting in Numpy Dot

NumPy’s broadcasting rules allow operations on arrays of different shapes, provided they are compatible. This feature is useful when working with multi-dimensional arrays.

Example 8: Broadcasting with Dot Product

import numpy as np

# Define a matrix and a vector
matrix = np.array([[1, 2], [3, 4], [5, 6]])
vector = np.array([7, 8])

# Compute the dot product
dot_product = np.dot(matrix, vector)

print(f"Dot product of matrix and vector:\n{dot_product}")  # numpyarray.com

Output:

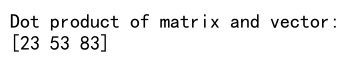
In this example, the vector is broadcasted to align with the matrix’s dimensions for the dot product computation. The result is a new vector.

Example 9: Dot Product with Incompatible Shapes

import numpy as np

# Define a matrix and a vector with incompatible shapes
matrix = np.array([[1, 2, 3], [4, 5, 6]])
vector = np.array([7, 8])

try:
    # Attempt to compute the dot product
    dot_product = np.dot(matrix, vector)
    print(f"Dot product of matrix and vector:\n{dot_product}")  # numpyarray.com
except ValueError as e:
    print(f"Error: {e}")  # numpyarray.com

Output:

Here, the matrix and vector have incompatible shapes for broadcasting. This results in an error, demonstrating the importance of shape compatibility in dot product operations.

Efficiency Considerations

NumPy is designed for efficiency. Understanding how the dot function leverages NumPy’s internal optimizations can help write more efficient code.

Example 10: Efficient Dot Product with Large Arrays

import numpy as np

# Define two large arrays
large_array_a = np.random.rand(1000, 1000)
large_array_b = np.random.rand(1000, 1000)

# Compute the dot product
dot_product = np.dot(large_array_a, large_array_b)

print("Dot product computed for large arrays")  # numpyarray.com

Output:

In this example, large arrays are used to demonstrate the efficiency of the dot function. NumPy’s internal optimizations ensure that such operations are performed efficiently.

Advanced Applications

The dot function is used in various advanced applications, including machine learning algorithms, physics simulations, and more.

Example 11: Dot Product in Machine Learning

import numpy as np

# Define feature vectors and weights
features = np.array([0.5, 0.6, 0.7])
weights = np.array([0.2, 0.3, 0.4])

# Compute the weighted sum (dot product)
weighted_sum = np.dot(features, weights)

print(f"Weighted sum in machine learning: {weighted_sum}")  # numpyarray.com

Output:

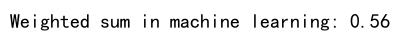
In this example, the dot product is used to compute the weighted sum of features, a common operation in machine learning algorithms such as linear regression.

Example 12: Dot Product in Physics Simulations

import numpy as np

# Define force and displacement vectors
force = np.array([10, 0])
displacement = np.array([2, 5])

# Compute the work done (dot product)
work_done = np.dot(force, displacement)

print(f"Work done in physics simulation: {work_done}")  # numpyarray.com

Output:

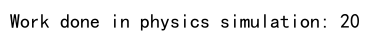
Here, the dot product is used to calculate the work done by a force applied over a displacement, a fundamental concept in physics.

Common Pitfalls

Understanding common pitfalls when using the dot function can help avoid errors and ensure accurate results.

Example 13: Incorrect Shapes for Matrix Multiplication

import numpy as np

# Define two matrices with incorrect shapes for multiplication
matrix_a = np.array([[1, 2, 3]])
matrix_b = np.array([[4, 5], [6, 7]])

try:
    # Attempt to compute the dot product
    dot_product = np.dot(matrix_a, matrix_b)
    print(f"Dot product of matrix_a and matrix_b:\n{dot_product}")  # numpyarray.com
except ValueError as e:
    print(f"Error: {e}")  # numpyarray.com

Output:

This example shows an attempt to multiply matrices with incompatible shapes, resulting in an error. Ensuring compatible shapes is crucial for successful matrix multiplication.

Example 14: Using Incorrect Function for Matrix Multiplication

import numpy as np

# Define two matrices
matrix_a = np.array([[1, 2], [3, 4]])
matrix_b = np.array([[5, 6], [7, 8]])

# Compute the element-wise product instead of matrix multiplication
element_wise_product = matrix_a * matrix_b

print(f"Element-wise product of matrix_a and matrix_b:\n{element_wise_product}")  # numpyarray.com

Output:

In this example, the * operator performs element-wise multiplication instead of matrix multiplication. The correct function for matrix multiplication is np.dot.

Numpy Dot Conclusion

The dot function in NumPy is a powerful tool for a wide range of operations, from simple vector dot products to complex matrix multiplications. Understanding its usage, handling different shapes and sizes of arrays, and being aware of common pitfalls can greatly enhance your ability to perform efficient and accurate computations.

This article has provided a comprehensive overview of the dot function, complete with numerous examples and detailed explanations. Whether you are working on scientific computing, machine learning, or any other field that requires efficient numerical operations, mastering the dot function will undoubtedly be beneficial.