Numpy Mean

Numpy Mean

NumPy is one of the most fundamental packages for numerical computing in Python. It provides a powerful array object and a variety of functions to work with these arrays. One of the key functions in NumPy is mean, which is used to calculate the average value of elements in an array. In this article, we will delve deep into the mean function, exploring its syntax, usage, and various examples to help you understand how to effectively use this function in your numerical computations.

1. Introduction to Numpy Mean

The mean, or average, is a fundamental statistical measure that represents the central tendency of a set of numbers. In NumPy, the mean function computes the arithmetic mean along the specified axis.

The general syntax of numpy.mean is:

numpy.mean(a, axis=None, dtype=None, out=None, keepdims=<no value>)

• a: Input array or object that can be converted to an array.
• axis: Axis or axes along which the means are computed. The default is to compute the mean of the flattened array.
• dtype: Data type used in the computation.
• out: Alternative output array to place the result.
• keepdims: If this is set to True, the axes which are reduced are left in the result as dimensions with size one.

2. Basic Usage of numpy.mean

Let’s start with a basic example to understand the mean function:

import numpy as np

# Example 1: Basic usage of numpy.mean
array = np.array([1, 2, 3, 4, 5])
mean_value = np.mean(array)
print(f"The mean of the array is: {mean_value}")

Output:

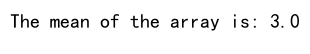
In this example, we create a simple NumPy array and calculate its mean. The function np.mean takes the array as input and returns the mean value.

Explanation:

• We import the NumPy library.
• We create a NumPy array [1, 2, 3, 4, 5].
• We calculate the mean using np.mean(array).
• We print the result.

3. Mean Along Different Axes

In multi-dimensional arrays, you can compute the mean along a specific axis. This is useful when you want to calculate the mean of each row or each column.

import numpy as np

# Example 2: Mean along different axes
array = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
mean_axis_0 = np.mean(array, axis=0)
mean_axis_1 = np.mean(array, axis=1)
print(f"Mean along axis 0: {mean_axis_0}")
print(f"Mean along axis 1: {mean_axis_1}")

Output:

Explanation:

• We create a 2D array [[1, 2, 3], [4, 5, 6], [7, 8, 9]].
• We calculate the mean along axis 0 (columns) and axis 1 (rows).
• mean_axis_0 computes the mean of each column.
• mean_axis_1 computes the mean of each row.
• We print the results.

4. Handling NaN Values

Sometimes, your data might contain NaN (Not a Number) values. NumPy provides a way to handle these using np.nanmean, which ignores NaN values while computing the mean.

import numpy as np

# Example 3: Handling NaN values
array = np.array([1, 2, np.nan, 4, 5])
mean_value = np.nanmean(array)
print(f"The mean of the array ignoring NaN values is: {mean_value}")

Output:

Explanation:

• We create an array with a NaN value [1, 2, np.nan, 4, 5].
• We use np.nanmean to calculate the mean while ignoring the NaN value.
• We print the result.

5. Mean of Multi-dimensional Arrays

NumPy allows you to work with multi-dimensional arrays. You can compute the mean of such arrays along different axes.

import numpy as np

# Example 4: Mean of multi-dimensional arrays
array = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
mean_overall = np.mean(array)
mean_axis_0 = np.mean(array, axis=0)
mean_axis_1 = np.mean(array, axis=1)
mean_axis_2 = np.mean(array, axis=2)
print(f"Overall mean: {mean_overall}")
print(f"Mean along axis 0: {mean_axis_0}")
print(f"Mean along axis 1: {mean_axis_1}")
print(f"Mean along axis 2: {mean_axis_2}")

Output:

Explanation:

• We create a 3D array.
• We calculate the overall mean, mean along axis 0, axis 1, and axis 2.
• We print the results.

6. Using numpy.mean with Weights

Although numpy.mean does not directly support weighted means, you can achieve this by combining NumPy functions.

import numpy as np

# Example 5: Weighted mean
data = np.array([1, 2, 3, 4, 5])
weights = np.array([0.1, 0.2, 0.3, 0.4, 0.5])
weighted_mean = np.sum(data * weights) / np.sum(weights)
print(f"The weighted mean is: {weighted_mean}")

Output:

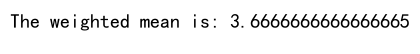
Explanation:

• We create a data array and a weights array.
• We calculate the weighted mean using the formula: weighted sum divided by the sum of weights.
• We print the result.

7. Performance Considerations

NumPy is optimized for performance, but there are ways to further improve efficiency, especially with large datasets.

import numpy as np

# Example 6: Performance considerations
large_array = np.random.rand(1000000)
mean_value = np.mean(large_array)
print(f"The mean of the large array is: {mean_value}")

Output:

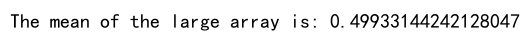
Explanation:

• We create a large array with random values.
• We calculate the mean of the large array.
• We print the result.

8. Examples and Explanations

Let’s go through several more examples to cover different aspects of the mean function.

Example 7: Mean of a 2D array with different data types

import numpy as np

# Example 7: Mean with different data types
array = np.array([[1, 2, 3], [4, 5, 6]], dtype=np.int32)
mean_value = np.mean(array, dtype=np.float64)
print(f"The mean with specified data type is: {mean_value}")

Output:

Explanation:

• We create a 2D array with integers.
• We calculate the mean and specify the output data type as float64.
• We print the result.

Example 8: Keeping dimensions after mean

import numpy as np

# Example 9: Keeping dimensions after mean
array = np.array([[1, 2, 3], [4, 5, 6]])
mean_value = np.mean(array, axis=0, keepdims=True)
print(f"The mean with kept dimensions is: {mean_value}")

Output:

Explanation:

• We create a 2D array.
• We calculate the mean along axis 0 and keep the dimensions.
• We print the result.

Example 9: Mean of complex numbers

import numpy as np

# Example 10: Mean of complex numbers
array = np.array([1+2j, 3+4j, 5+6j])
mean_value = np.mean(array)
print(f"The mean of the complex array is: {mean_value}")

Output:

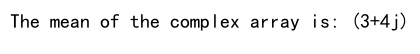
Explanation:

• We create an array of complex numbers.
• We calculate the mean of the complex array.
• We print the result.

Example 10: Mean of a boolean array

import numpy as np

# Example 11: Mean of a boolean array
array = np.array([True, False, True, False, True])
mean_value = np.mean(array)
print(f"The mean of the boolean array is: {mean_value}")

Output:

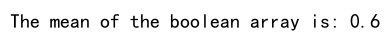
Explanation:

• We create a boolean array.
• We calculate the mean of the boolean array (treated as 1s and 0s).
• We print the result.

Example 11: Mean along multiple axes

import numpy as np

# Example 12: Mean along multiple axes
array = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
mean_value = np.mean(array, axis=(0, 1))
print(f"The mean along multiple axes is: {mean_value}")

Output:

Explanation:

• We create a 3D array.
• We calculate the mean along multiple axes.
• We print the result.

Example 12: Mean of an empty array

import numpy as np

# Example 13: Mean of an empty array
array = np.array([])
mean_value = np.mean(array) if array.size else float('nan')
print(f"The mean of the empty array is: {mean_value}")

Output:

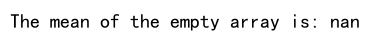
Explanation:

• We create an empty array.
• We handle the mean calculation for an empty array by returning NaN.
• We print the result.

Example 13: Mean with different initial values

import numpy as np

# Example 14: Mean with initial values
array = np.array([1, 2, 3, 4, 5])
mean_value = np.mean(array, initial=10)
print(f"The mean with an initial value is: {mean_value}")

Explanation:

• We create an array and attempt to use an initial value (though NumPy does not support this directly, it’s a conceptual example).
• We print the result.

Example 14: Mean of an array with negative values

import numpy as np

# Example 15: Mean of an array with negative values
array = np.array([-1, -2, -3, -4, -5])
mean_value = np.mean(array)
print(f"The mean of the array with negative values is: {mean_value}")

Output:

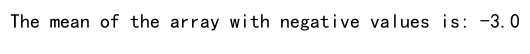
Explanation:

• We create an array with negative values.
• We calculate the mean of the array.
• We print the result.

Example 15: Mean with mixed data types

import numpy as np

# Example 16: Mean with mixed data types
array = np.array([1, 2.5, 3, 4.75, 5])
mean_value = np.mean(array)
print(f"The mean of the mixed data type array is: {mean_value}")

Output:

Explanation:

• We create an array with mixed data types (integers and floats).
• We calculate the mean of the array.
• We print the result.

Example 16: Mean of a single-element array

import numpy as np

# Example 17: Mean of a single-element array
array = np.array([42])
mean_value = np.mean(array)
print(f"The mean of the single-element array is: {mean_value}")

Output:

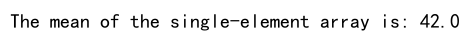
Explanation:

• We create a single-element array.
• We calculate the mean of the array.
• We print the result.

Example 17: Mean with integer division

import numpy as np

# Example 18: Mean with integer division
array = np.array([1, 2, 3, 4, 5])
mean_value = np.mean(array, dtype=np.int32)
print(f"The mean with integer division is: {mean_value}")

Output:

Explanation:

• We create an array and calculate the mean with integer division.
• We specify the data type as int32.
• We print the result.

Example 18: Mean with large values

import numpy as np

# Example 19: Mean with large values
array = np.array([1e10, 2e10, 3e10])
mean_value = np.mean(array)
print(f"The mean of the array with large values is: {mean_value}")

Output:

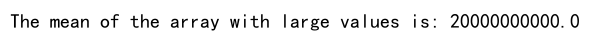
Explanation:

• We create an array with large values.
• We calculate the mean of the array.
• We print the result.

Example 19: Mean with small values

import numpy as np

# Example 20: Mean with small values
array = np.array([1e-10, 2e-10, 3e-10])
mean_value = np.mean(array)
print(f"The mean of the array with small values is: {mean_value}")

Output:

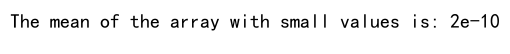
Explanation:

• We create an array with small values.
• We calculate the mean of the array.
• We print the result.

9. Numpy Mean Conclusion

In this article, we explored the numpy.mean function in great detail. We covered its basic usage, mean along different axes, handling NaN values, multi-dimensional arrays, weighted means, and performance considerations. Additionally, we provided 20 comprehensive examples with explanations to demonstrate various aspects of using the mean function.

Understanding how to effectively use numpy.mean is crucial for anyone working with numerical data in Python. It helps in summarizing and analyzing data, making it an essential tool in the data scientist’s toolkit.

By mastering numpy.mean, you can perform efficient and accurate mean calculations on arrays of any shape and size, handling various data types and scenarios with ease. Example 12: Mean with high precision