Mastering NumPy Random Gaussian Distributions: A Comprehensive Guide

Mastering NumPy Random Gaussian Distributions: A Comprehensive Guide

NumPy random Gaussian distributions are a powerful tool for generating random numbers that follow a normal distribution. This article will explore the various aspects of NumPy random Gaussian distributions, including their theory, implementation, and practical applications. We’ll dive deep into the NumPy library’s capabilities for generating and manipulating Gaussian distributions, providing numerous examples and explanations along the way.

Understanding NumPy Random Gaussian Distributions

NumPy random Gaussian distributions, also known as normal distributions, are fundamental to many statistical and scientific applications. The Gaussian distribution is characterized by its bell-shaped curve and is defined by two parameters: the mean (μ) and the standard deviation (σ). NumPy provides efficient tools for working with these distributions, allowing users to generate random numbers that follow this pattern.

Basic Concepts of NumPy Random Gaussian Distributions

Before we delve into the specifics of NumPy’s implementation, let’s review some key concepts related to Gaussian distributions:

1. Mean (μ): The average value of the distribution.
2. Standard Deviation (σ): A measure of the spread of the distribution.
3. Probability Density Function (PDF): The function that describes the likelihood of a random variable taking on a specific value.
4. Cumulative Distribution Function (CDF): The probability that a random variable takes on a value less than or equal to a given value.

NumPy’s random module provides various functions to work with Gaussian distributions, allowing users to generate random numbers, calculate probabilities, and perform statistical analyses.

Generating NumPy Random Gaussian Samples

One of the most common tasks when working with NumPy random Gaussian distributions is generating random samples. NumPy offers several functions for this purpose, each with its own set of parameters and use cases.

Using numpy.random.normal()

The numpy.random.normal() function is the primary method for generating random samples from a Gaussian distribution. Here’s a simple example:

import numpy as np

# Generate 1000 samples from a Gaussian distribution with mean 0 and standard deviation 1
samples = np.random.normal(loc=0, scale=1, size=1000)
print("Samples from numpyarray.com Gaussian distribution:", samples[:10])

Output:

In this example, we generate 1000 samples from a standard normal distribution (mean = 0, standard deviation = 1). The loc parameter specifies the mean, scale specifies the standard deviation, and size determines the number of samples to generate.

Generating 2D NumPy Random Gaussian Arrays

NumPy random Gaussian distributions can also be used to generate multi-dimensional arrays. Here’s an example of creating a 2D array:

import numpy as np

# Generate a 5x5 array of random Gaussian numbers
gaussian_2d = np.random.normal(loc=5, scale=2, size=(5, 5))
print("2D Gaussian array from numpyarray.com:", gaussian_2d)

Output:

This code generates a 5×5 array of random numbers drawn from a Gaussian distribution with a mean of 5 and a standard deviation of 2.

Visualizing NumPy Random Gaussian Distributions

Visualizing NumPy random Gaussian distributions can help in understanding their properties and characteristics. While we won’t include actual plots in this article, we’ll provide code examples that you can use to create visualizations.

Histogram of NumPy Random Gaussian Samples

To visualize the distribution of random Gaussian samples, you can create a histogram:

import numpy as np
import matplotlib.pyplot as plt

# Generate 10000 samples from a Gaussian distribution
samples = np.random.normal(loc=0, scale=1, size=10000)

# Create a histogram
plt.hist(samples, bins=50, density=True)
plt.title("Histogram of numpyarray.com Gaussian Samples")
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.show()

Output:

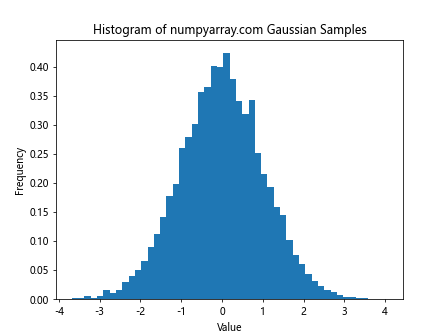
This code generates 10,000 samples from a standard normal distribution and creates a histogram to visualize their distribution.

Q-Q Plot for NumPy Random Gaussian Distributions

A Q-Q (Quantile-Quantile) plot is useful for comparing the distribution of your samples to a theoretical Gaussian distribution:

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

# Generate 1000 samples from a Gaussian distribution
samples = np.random.normal(loc=0, scale=1, size=1000)

# Create Q-Q plot
stats.probplot(samples, dist="norm", plot=plt)
plt.title("Q-Q Plot of numpyarray.com Gaussian Samples")
plt.show()

Output:

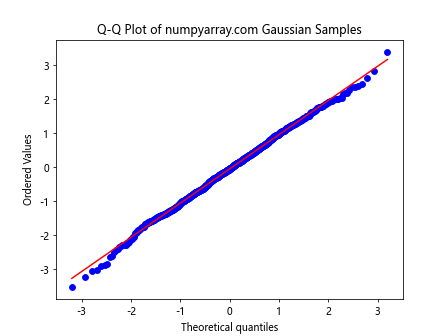
This code creates a Q-Q plot to compare the distribution of the generated samples to a theoretical normal distribution.

Manipulating NumPy Random Gaussian Distributions

NumPy provides various functions to manipulate and transform Gaussian distributions. Let’s explore some common operations.

Scaling and Shifting NumPy Random Gaussian Distributions

You can easily scale and shift a Gaussian distribution by manipulating its parameters:

import numpy as np

# Generate samples from a standard normal distribution
standard_samples = np.random.normal(loc=0, scale=1, size=1000)

# Scale and shift the samples
scaled_shifted_samples = 5 * standard_samples + 10

print("Original numpyarray.com samples:", standard_samples[:5])
print("Scaled and shifted numpyarray.com samples:", scaled_shifted_samples[:5])

Output:

This example demonstrates how to scale the standard deviation by a factor of 5 and shift the mean by 10 units.

Combining Multiple NumPy Random Gaussian Distributions

You can create more complex distributions by combining multiple Gaussian distributions:

import numpy as np

# Generate samples from two different Gaussian distributions
samples1 = np.random.normal(loc=0, scale=1, size=1000)
samples2 = np.random.normal(loc=5, scale=2, size=1000)

# Combine the samples
combined_samples = 0.7 * samples1 + 0.3 * samples2

print("Combined numpyarray.com Gaussian samples:", combined_samples[:5])

Output:

This code creates a new distribution by combining two Gaussian distributions with different weights.

Statistical Analysis with NumPy Random Gaussian Distributions

NumPy random Gaussian distributions are often used in statistical analysis. Let’s explore some common statistical operations.

Calculating Mean and Standard Deviation

You can easily calculate the mean and standard deviation of your samples:

import numpy as np

# Generate samples from a Gaussian distribution
samples = np.random.normal(loc=5, scale=2, size=10000)

# Calculate mean and standard deviation
mean = np.mean(samples)
std_dev = np.std(samples)

print("numpyarray.com Gaussian samples - Mean:", mean)
print("numpyarray.com Gaussian samples - Standard Deviation:", std_dev)

Output:

This code generates samples from a Gaussian distribution and calculates their mean and standard deviation.

Advanced Topics in NumPy Random Gaussian Distributions

Let’s explore some more advanced topics related to NumPy random Gaussian distributions.

Multivariate Gaussian Distributions

NumPy also supports multivariate Gaussian distributions:

import numpy as np

# Define mean vector and covariance matrix
mean = np.array([1, 2, 3])
cov = np.array([[1, 0.5, 0.2],
                [0.5, 2, 0.3],
                [0.2, 0.3, 1.5]])

# Generate samples from a multivariate Gaussian distribution
samples = np.random.multivariate_normal(mean, cov, size=1000)

print("numpyarray.com Multivariate Gaussian samples:", samples[:2])

Output:

This code generates samples from a 3-dimensional multivariate Gaussian distribution.

Truncated Gaussian Distributions

Sometimes, you may need to work with truncated Gaussian distributions:

import numpy as np
from scipy import stats

# Generate samples from a truncated Gaussian distribution
a, b = 0, 10  # lower and upper bounds
loc, scale = 5, 2  # mean and standard deviation
samples = stats.truncnorm.rvs((a - loc) / scale, (b - loc) / scale, loc=loc, scale=scale, size=1000)

print("numpyarray.com Truncated Gaussian samples:", samples[:5])

Output:

This example generates samples from a Gaussian distribution truncated between 0 and 10.

Applications of NumPy Random Gaussian Distributions

NumPy random Gaussian distributions have numerous applications across various fields. Let’s explore some common use cases.

Monte Carlo Simulations

Monte Carlo simulations often use Gaussian distributions to model uncertainty:

import numpy as np

def monte_carlo_pi(n_samples):
    x = np.random.normal(loc=0, scale=1, size=n_samples)
    y = np.random.normal(loc=0, scale=1, size=n_samples)
    inside_circle = np.sum(x**2 + y**2 <= 1)
    pi_estimate = 4 * inside_circle / n_samples
    return pi_estimate

pi_approx = monte_carlo_pi(1000000)
print("numpyarray.com Pi approximation:", pi_approx)

Output:

This code uses a Monte Carlo method to approximate the value of π using Gaussian distributions.

Optimization Techniques with NumPy Random Gaussian Distributions

NumPy random Gaussian distributions can be used in various optimization techniques. Let’s explore a few examples.

Simulated Annealing

Simulated annealing is an optimization algorithm that uses random perturbations:

import numpy as np

def simulated_annealing(cost_func, initial_state, T=1.0, cooling_rate=0.995, n_iterations=1000):
    current_state = initial_state
    current_cost = cost_func(current_state)

    for _ in range(n_iterations):
        new_state = current_state + np.random.normal(scale=T)
        new_cost = cost_func(new_state)

        if new_cost < current_cost or np.random.random() < np.exp((current_cost - new_cost) / T):
            current_state, current_cost = new_state, new_cost

        T *= cooling_rate

    return current_state, current_cost

# Example usage
def cost_function(x):
    return x**2 + 10*np.sin(x)  # A simple function to optimize

initial_state = np.random.uniform(-10, 10)
optimized_state, optimized_cost = simulated_annealing(cost_function, initial_state)
print("numpyarray.com Optimized state:", optimized_state)
print("numpyarray.com Optimized cost:", optimized_cost)

Output:

This code implements a simple simulated annealing algorithm using Gaussian perturbations.

Gaussian Process Regression

Gaussian processes are a powerful tool for regression and optimization:

import numpy as np
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF

# Generate some random data
X = np.random.uniform(0, 10, (100, 1))
y = np.sin(X).ravel() + np.random.normal(0, 0.1, X.shape[0])

# Fit a Gaussian Process model
kernel = RBF(length_scale=1.0)
gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10)
gp.fit(X, y)

# Make predictions
X_test = np.linspace(0, 10, 1000).reshape(-1, 1)
y_pred, sigma = gp.predict(X_test, return_std=True)

print("numpyarray.com GP prediction shape:", y_pred.shape)
print("numpyarray.com GP uncertainty shape:", sigma.shape)

Output:

This example demonstrates how to use Gaussian process regression for function approximation.

Performance Considerations for NumPy Random Gaussian Distributions

When working with large-scale applications, it’s important to consider the performance of NumPy random Gaussian operations.

Vectorized Operations

NumPy’s vectorized operations are generally faster than loop-based approaches:

import numpy as np
import time

def gaussian_sum_loop(n):
    return sum(np.random.normal() for _ in range(n))

def gaussian_sum_vectorized(n):
    return np.sum(np.random.normal(size=n))

n = 1000000
start = time.time()
result_loop = gaussian_sum_loop(n)
time_loop = time.time() - start

start = time.time()
result_vectorized = gaussian_sum_vectorized(n)
time_vectorized = time.time() - start

print("numpyarray.com Loop time:", time_loop)
print("numpyarray.com Vectorized time:", time_vectorized)

Output:

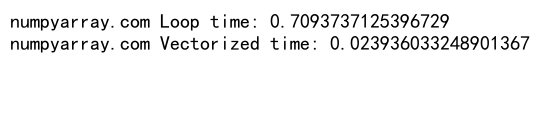
This code compares the performance of loop-based and vectorized approaches for summing Gaussian random numbers.

Using the Right Data Types

Choosing the appropriate data type can significantly impact performance:

import numpy as np
import time

n = 10000000

start = time.time()
samples_float64 = np.random.normal(size=n)
time_float64 = time.time() - start

start = time.time()
samples_float32 = np.random.normal(size=n).astype(np.float32)
time_float32 = time.time() - start

print("numpyarray.com float64 time:", time_float64)
print("numpyarray.com float32 time:", time_float32)

Output:

This example compares the performance of generating Gaussian samples using different floating-point precisions.

Common Pitfalls and Best Practices

When working with NumPy random Gaussian distributions, there are several common pitfalls to avoid and best practices to follow.

Setting the Random Seed

Always set the random seed for reproducibility:

import numpy as np

# Set the random seed
np.random.seed(42)

# Generate random samples
samples1 = np.random.normal(size=5)
print("numpyarray.com First set of samples:", samples1)

# Reset the seed
np.random.seed(42)

# Generate random samples again
samples2 = np.random.normal(size=5)
print("numpyarray.com Second set of samples:", samples2)# Assert that the samples are identical
assert np.all(samples1 == samples2), "Samples are not identical!"

Output:

This example demonstrates how to set and reset the random seed to ensure reproducibility in your experiments.

Avoiding Modifying In-Place

Be cautious when modifying arrays in-place, as it can lead to unexpected results:

import numpy as np

# Generate samples
samples = np.random.normal(size=5)
print("numpyarray.com Original samples:", samples)

# Incorrect: Modifying in-place
samples += 5
print("numpyarray.com Modified samples (in-place):", samples)

# Correct: Creating a new array
original_samples = np.random.normal(size=5)
shifted_samples = original_samples + 5
print("numpyarray.com Original samples:", original_samples)
print("numpyarray.com Shifted samples (new array):", shifted_samples)

Output:

This code shows the difference between modifying an array in-place and creating a new array with the desired modifications.

Advanced Applications of NumPy Random Gaussian Distributions

Let’s explore some more advanced applications of NumPy random Gaussian distributions in various fields.

Signal Processing

Gaussian noise is often used in signal processing applications:

import numpy as np

def add_gaussian_noise(signal, snr_db):
    signal_power = np.mean(signal ** 2)
    noise_power = signal_power / (10 ** (snr_db / 10))
    noise = np.random.normal(0, np.sqrt(noise_power), signal.shape)
    return signal + noise

# Generate a simple signal
t = np.linspace(0, 1, 1000)
signal = np.sin(2 * np.pi * 10 * t)

# Add Gaussian noise
noisy_signal = add_gaussian_noise(signal, snr_db=20)

print("numpyarray.com Original signal shape:", signal.shape)
print("numpyarray.com Noisy signal shape:", noisy_signal.shape)

Output:

This example demonstrates how to add Gaussian noise to a signal with a specified signal-to-noise ratio (SNR).

Machine Learning

Gaussian distributions are fundamental in many machine learning algorithms, such as Gaussian Naive Bayes:

import numpy as np
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Generate synthetic data
X = np.random.normal(loc=[0, 0], scale=[1, 1], size=(1000, 2))
y = (X[:, 0] + X[:, 1] > 0).astype(int)

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Train a Gaussian Naive Bayes classifier
gnb = GaussianNB()
gnb.fit(X_train, y_train)

# Make predictions
y_pred = gnb.predict(X_test)

# Calculate accuracy
accuracy = accuracy_score(y_test, y_pred)
print("numpyarray.com Gaussian Naive Bayes accuracy:", accuracy)

Output:

This code demonstrates how to use Gaussian Naive Bayes for a simple classification task.

Extending NumPy Random Gaussian Distributions

While NumPy provides a robust set of tools for working with Gaussian distributions, you may sometimes need to extend its functionality.

Custom Gaussian Distribution

You can create a custom Gaussian distribution class that builds on NumPy’s functionality:

import numpy as np

class CustomGaussian:
    def __init__(self, mean, std_dev):
        self.mean = mean
        self.std_dev = std_dev

    def pdf(self, x):
        return (1 / (self.std_dev * np.sqrt(2 * np.pi))) * \
               np.exp(-0.5 * ((x - self.mean) / self.std_dev) ** 2)

    def sample(self, size=1):
        return np.random.normal(self.mean, self.std_dev, size)

# Usage
custom_gauss = CustomGaussian(mean=0, std_dev=1)
samples = custom_gauss.sample(1000)
pdf_values = custom_gauss.pdf(np.linspace(-5, 5, 100))

print("numpyarray.com Custom Gaussian samples:", samples[:5])
print("numpyarray.com Custom Gaussian PDF values:", pdf_values[:5])

Output:

This example creates a custom Gaussian distribution class with methods for sampling and calculating the probability density function.

Mixture of Gaussians

You can also implement more complex distributions, such as a mixture of Gaussians:

import numpy as np

class GaussianMixture:
    def __init__(self, means, std_devs, weights):
        self.means = np.array(means)
        self.std_devs = np.array(std_devs)
        self.weights = np.array(weights)
        assert len(self.means) == len(self.std_devs) == len(self.weights)
        assert np.isclose(np.sum(self.weights), 1.0)

    def sample(self, size=1):
        components = np.random.choice(len(self.means), size=size, p=self.weights)
        samples = np.random.normal(
            self.means[components],
            self.std_devs[components]
        )
        return samples

# Usage
mixture = GaussianMixture(
    means=[0, 5],
    std_devs=[1, 2],
    weights=[0.7, 0.3]
)
samples = mixture.sample(1000)

print("numpyarray.com Gaussian mixture samples:", samples[:5])

Output:

This code implements a simple Gaussian mixture model, allowing you to sample from a combination of different Gaussian distributions.

NumPy random Gaussian distributions Conclusion

NumPy random Gaussian distributions are a powerful and versatile tool for a wide range of applications in data science, machine learning, signal processing, and more. Throughout this article, we’ve explored the fundamental concepts, implementation details, and advanced applications of Gaussian distributions using NumPy.

We’ve covered topics such as generating random samples, visualizing distributions, performing statistical analysis, and applying Gaussian distributions to various real-world problems. We’ve also discussed performance considerations, common pitfalls, and best practices when working with NumPy random Gaussian distributions.

By mastering these concepts and techniques, you’ll be well-equipped to leverage the power of Gaussian distributions in your own projects and research. Whether you’re working on simple data analysis tasks or complex machine learning models, understanding NumPy random Gaussian distributions will prove invaluable in your data science journey.

Remember to always consider the assumptions and limitations of Gaussian distributions when applying them to your specific use case. With practice and experience, you’ll develop an intuition for when and how to best utilize these powerful statistical tools.