Numpy Array
Numpy is a fundamental package for scientific computing in Python. It provides support for large, multi-dimensional arrays and matrices, along with a large collection of high-level mathematical functions to operate on these arrays. This article will delve into the intricacies of Numpy arrays, providing a comprehensive guide on their capabilities and functionalities. We will explore various aspects of Numpy arrays through detailed examples, ensuring each code snippet is self-contained and executable.
Introduction to Numpy Arrays
A Numpy array is a grid of values, all of the same type, and is indexed by a tuple of nonnegative integers. The number of dimensions is the rank of the array; the shape of an array is a tuple of integers giving the size of the array along each dimension.
Creating Numpy Arrays
Numpy arrays can be created from Python lists or tuples using the numpy.array function.
import numpy as np
# Create a numpy array from a list
array_from_list = np.array([1, 2, 3, 4, 5])
print(array_from_list)
# Create a numpy array from a tuple
array_from_tuple = np.array((6, 7, 8, 9, 10))
print(array_from_tuple)
Output:
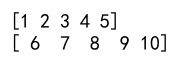
Specifying the Data Type
When creating a Numpy array, you can specify the data type using the dtype parameter. This is useful when you need precise control over how data is stored in memory and on disk, especially for large data sets.
import numpy as np
# Create an array of integers
int_array = np.array([1, 2, 3, 4], dtype=np.int32)
print(int_array)
# Create an array of floats
float_array = np.array([1, 2, 3, 4], dtype=np.float64)
print(float_array)
Output:

Operations on Numpy Arrays
Numpy provides a wide range of mathematical functions that can be performed on arrays. These include operations such as addition, multiplication, and more complex functions like matrix multiplication.
Basic Arithmetic Operations
You can perform element-wise arithmetic operations directly on Numpy arrays.
import numpy as np
a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
# Element-wise addition
c = a + b
print(c)
# Element-wise subtraction
d = b - a
print(d)
# Element-wise multiplication
e = a * b
print(e)
# Element-wise division
f = b / a
print(f)
Output:

Advanced Mathematical Functions
Numpy supports a variety of complex mathematical operations, such as trigonometric functions, exponential functions, and logarithms.
import numpy as np
# Create an array
x = np.array([0, np.pi/2, np.pi])
# Trigonometric functions
sin_x = np.sin(x)
print(sin_x)
# Exponential function
exp_x = np.exp(x)
print(exp_x)
# Natural logarithm
log_x = np.log(x[1:])
print(log_x)
Output:

Array Indexing and Slicing
Indexing and slicing are essential for accessing subarrays and individual elements in Numpy arrays.
Indexing
You can access an array element by referring to its index number. The indexes in Numpy arrays start with 0, meaning that the first element has an index of 0.
import numpy as np
arr = np.array([10, 20, 30, 40, 50])
# Access the first element
print(arr[0])
# Access the last element
print(arr[-1])
Output:
![]()
Slicing
Slicing in Python means taking elements from one given index to another given index.
import numpy as np
arr = np.array([10, 20, 30, 40, 50, 60, 70, 80, 90, 100])
# Slice elements from index 3 to index 7
print(arr[3:8])
# Slice elements from the beginning to index 5
print(arr[:6])
# Slice elements from index 4 to the end
print(arr[4:])
Output:

Reshaping Arrays
Reshaping allows you to change the shape of an existing array without changing its data.
import numpy as np
# Create an array with 10 elements
arr = np.arange(10)
print(arr)
# Reshape it to 2x5
reshaped_arr = arr.reshape(2, 5)
print(reshaped_arr)
Output:
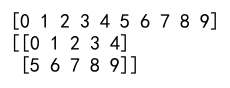
Broadcasting
Broadcasting is a powerful mechanism that allows numpy to work with arrays of different shapes when performing arithmetic operations.
import numpy as np
a = np.array([1, 2, 3])
b = np.array([[0], [1], [2]])
# Broadcasting example
c = a + b
print(c)
Output:

Linear Algebra
Numpy is highly capable in performing linear algebra operations, making it useful for data science and machine learning applications.
Matrix Multiplication
import numpy as np
# Define two matrices
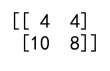
A = np.array([[1, 2], [3, 4]])
B = np.array([[2, 0], [1, 2]])
# Matrix multiplication
C = np.dot(A, B)
print(C)
Output:
Eigenvalues and Eigenvectors
import numpy as np
# Define a matrix
A = np.array([[4, 2], [1, 3]])
# Compute eigenvalues and eigenvectors
eigenvalues, eigenvectors = np.linalg.eig(A)
print(eigenvalues)
print(eigenvectors)
Output:

Numpy Array Conclusion
This article has explored the fundamental concepts and operations associated with Numpy arrays. Through numerous examples, we have demonstrated how to create, manipulate, and perform complex mathematical operations on Numpy arrays. These capabilities make Numpy an indispensable tool for anyone working in scientific computing, data analysis, or machine learning.