Mastering NumPy Random Binomial Distribution: A Comprehensive Guide

Mastering NumPy Random Binomial Distribution: A Comprehensive Guide

NumPy random binomial distribution is a powerful tool for generating random samples from a binomial distribution. This article will explore the various aspects of NumPy random binomial distribution, including its definition, usage, and practical applications. We’ll dive deep into the numpy.random.binomial() function and provide numerous examples to illustrate its functionality.

Understanding NumPy Random Binomial Distribution

NumPy random binomial distribution is based on the binomial distribution, which models the number of successes in a fixed number of independent Bernoulli trials. The numpy.random.binomial() function in NumPy allows us to generate random samples from this distribution.

Definition of NumPy Random Binomial Distribution

The NumPy random binomial distribution is characterized by two parameters:

1. n: The number of trials
2. p: The probability of success for each trial

The function returns the number of successes in these n trials.

Syntax of numpy.random.binomial()

The basic syntax for using the NumPy random binomial function is:

numpy.random.binomial(n, p, size=None)

Where:
– n: Number of trials (non-negative integer)
– p: Probability of success (float between 0 and 1)
– size: Output shape (optional)

Let’s look at a simple example:

import numpy as np

# Generate a single random sample
result = np.random.binomial(n=10, p=0.5)
print("numpyarray.com - Single sample:", result)

Output:

This code generates a single random sample from a binomial distribution with 10 trials and a success probability of 0.5.

Generating Multiple Samples with NumPy Random Binomial

One of the powerful features of NumPy random binomial is the ability to generate multiple samples at once. This is particularly useful for simulations and statistical analysis.

Using the ‘size’ Parameter

The ‘size’ parameter allows us to specify the shape of the output array. Let’s generate a 1D array of samples:

import numpy as np

# Generate 5 random samples
results = np.random.binomial(n=10, p=0.5, size=5)
print("numpyarray.com - Multiple samples:", results)

Output:

This code generates 5 random samples, each representing the number of successes in 10 trials with a success probability of 0.5.

Generating 2D Arrays of Samples

We can also generate 2D arrays of samples:

import numpy as np

# Generate a 3x4 array of random samples
results_2d = np.random.binomial(n=10, p=0.5, size=(3, 4))
print("numpyarray.com - 2D array of samples:")
print(results_2d)

Output:

This code generates a 3×4 array of random samples from the binomial distribution.

Varying Parameters in NumPy Random Binomial

The NumPy random binomial function allows us to vary the parameters n and p across different trials.

Varying the Number of Trials (n)

We can provide an array of different n values:

import numpy as np

n_values = [5, 10, 15, 20]
results = np.random.binomial(n=n_values, p=0.5)
print("numpyarray.com - Varying n:", results)

Output:

This code generates random samples with different numbers of trials for each sample.

Varying the Probability of Success (p)

Similarly, we can vary the probability of success:

import numpy as np

p_values = [0.1, 0.3, 0.5, 0.7]
results = np.random.binomial(n=10, p=p_values)
print("numpyarray.com - Varying p:", results)

Output:

This code generates random samples with different probabilities of success for each sample.

Practical Applications of NumPy Random Binomial

NumPy random binomial has numerous practical applications in various fields. Let’s explore some of them.

Simulating Coin Flips

We can use NumPy random binomial to simulate coin flips:

import numpy as np

# Simulate 1000 coin flips
coin_flips = np.random.binomial(n=1, p=0.5, size=1000)
heads_count = np.sum(coin_flips)
print(f"numpyarray.com - Number of heads in 1000 flips: {heads_count}")

Output:

This code simulates 1000 coin flips and counts the number of heads.

Modeling Disease Spread

NumPy random binomial can be used to model the spread of a disease:

import numpy as np

population = 10000
infection_rate = 0.01
infected = np.random.binomial(n=population, p=infection_rate)
print(f"numpyarray.com - Number of infected people: {infected}")

Output:

This code models the number of people infected in a population of 10,000 with an infection rate of 1%.

Advanced Techniques with NumPy Random Binomial

Let’s explore some advanced techniques using NumPy random binomial.

Combining with Other NumPy Functions

We can combine NumPy random binomial with other NumPy functions for more complex operations:

import numpy as np

# Generate 1000 samples and calculate mean and standard deviation
samples = np.random.binomial(n=20, p=0.6, size=1000)
mean = np.mean(samples)
std = np.std(samples)
print(f"numpyarray.com - Mean: {mean}, Standard Deviation: {std}")

Output:

This code generates 1000 samples and calculates their mean and standard deviation.

Using NumPy Random Binomial in Custom Functions

We can create custom functions that utilize NumPy random binomial:

import numpy as np

def simulate_exam_scores(num_students, num_questions, passing_probability):
    scores = np.random.binomial(n=num_questions, p=passing_probability, size=num_students)
    return scores

exam_scores = simulate_exam_scores(100, 50, 0.7)
print("numpyarray.com - First 10 exam scores:", exam_scores[:10])

Output:

This custom function simulates exam scores for a given number of students.

Comparing NumPy Random Binomial with Theoretical Probabilities

It’s often useful to compare the results of NumPy random binomial with theoretical probabilities.

Plotting Histogram of Samples

We can create a histogram of the samples and compare it with the theoretical probability mass function:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom

n, p = 20, 0.6
samples = np.random.binomial(n, p, size=10000)

x = np.arange(0, n+1)
pmf = binom.pmf(x, n, p)

plt.hist(samples, bins=n+1, density=True, alpha=0.7, label='Samples')
plt.plot(x, pmf, 'ro-', label='Theoretical PMF')
plt.title('numpyarray.com - Binomial Distribution: Samples vs Theoretical')
plt.xlabel('Number of Successes')
plt.ylabel('Probability')
plt.legend()
plt.show()

Output:

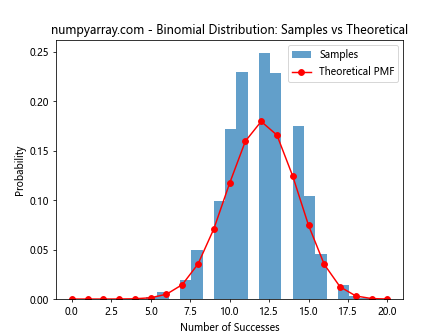
This code generates a histogram of 10,000 samples and compares it with the theoretical probability mass function.

Error Handling in NumPy Random Binomial

It’s important to handle potential errors when using NumPy random binomial.

Handling Invalid Input

Let’s see how to handle invalid input:

import numpy as np

try:
    result = np.random.binomial(n=-5, p=0.5)
except ValueError as e:
    print("numpyarray.com - Error:", str(e))

try:
    result = np.random.binomial(n=10, p=1.5)
except ValueError as e:
    print("numpyarray.com - Error:", str(e))

Output:

This code demonstrates how NumPy handles invalid input for n and p parameters.

NumPy Random Binomial in Data Analysis

NumPy random binomial is often used in data analysis tasks. Let’s explore a few examples.

Simulating A/B Testing

We can use NumPy random binomial to simulate A/B testing:

import numpy as np

def ab_test_simulation(n_visitors, p_control, p_treatment):
    control = np.random.binomial(n=n_visitors, p=p_control)
    treatment = np.random.binomial(n=n_visitors, p=p_treatment)
    return control, treatment

control, treatment = ab_test_simulation(1000, 0.1, 0.15)
print(f"numpyarray.com - Control conversions: {control}, Treatment conversions: {treatment}")

Output:

This code simulates an A/B test with 1000 visitors in each group.

Bootstrapping with NumPy Random Binomial

NumPy random binomial can be used for bootstrapping:

import numpy as np

def bootstrap_mean(data, num_bootstrap_samples):
    bootstrap_means = np.zeros(num_bootstrap_samples)
    for i in range(num_bootstrap_samples):
        bootstrap_sample = np.random.choice(data, size=len(data), replace=True)
        bootstrap_means[i] = np.mean(bootstrap_sample)
    return bootstrap_means

original_data = np.random.binomial(n=10, p=0.6, size=100)
bootstrap_results = bootstrap_mean(original_data, 1000)
confidence_interval = np.percentile(bootstrap_results, [2.5, 97.5])
print(f"numpyarray.com - 95% Confidence Interval: {confidence_interval}")

Output:

This code demonstrates bootstrapping using NumPy random binomial to generate the original data.

Performance Considerations with NumPy Random Binomial

When working with large datasets or performing many simulations, performance becomes crucial.

Vectorization with NumPy Random Binomial

Vectorization can significantly improve performance:

import numpy as np
import time

def slow_binomial(n, p, size):
    return np.array([np.random.binomial(n, p) for _ in range(size)])

def fast_binomial(n, p, size):
    return np.random.binomial(n, p, size)

size = 1000000
n, p = 10, 0.5

start = time.time()
slow_result = slow_binomial(n, p, size)
slow_time = time.time() - start

start = time.time()
fast_result = fast_binomial(n, p, size)
fast_time = time.time() - start

print(f"numpyarray.com - Slow method time: {slow_time:.4f}s")
print(f"numpyarray.com - Fast method time: {fast_time:.4f}s")

Output:

This code compares the performance of a loop-based approach with the vectorized NumPy random binomial function.

NumPy Random Binomial in Machine Learning

NumPy random binomial has applications in machine learning, particularly in creating synthetic datasets and data augmentation.

Generating Synthetic Binary Classification Data

We can use NumPy random binomial to generate synthetic binary classification data:

import numpy as np

def generate_binary_classification_data(n_samples, n_features, class_sep=1.0):
    X = np.random.randn(n_samples, n_features)
    y = np.random.binomial(n=1, p=0.5, size=n_samples)
    X[y == 1] += class_sep
    return X, y

X, y = generate_binary_classification_data(1000, 2)
print("numpyarray.com - First 5 samples:")
print(X[:5])
print("numpyarray.com - First 5 labels:")
print(y[:5])

Output:

This code generates synthetic binary classification data using NumPy random binomial for the labels.

NumPy random binomial Conclusion

NumPy random binomial is a versatile tool for generating random samples from a binomial distribution. Its applications span various fields, including statistics, data analysis, and machine learning. By mastering NumPy random binomial, you can enhance your ability to model and analyze binary outcomes in your data science projects.

Remember to consider the parameters n and p carefully when using NumPy random binomial, as they directly affect the distribution of your random samples. Always validate your inputs and handle potential errors to ensure robust code.

Whether you’re simulating coin flips, modeling disease spread, or generating synthetic datasets, NumPy random binomial provides a powerful and efficient way to work with binomial distributions in your Python projects.