Numpy Array Dimensions

Numpy Array Dimensions

Understanding the dimensions of arrays in NumPy is crucial for anyone working with data in Python, as it affects how data is structured, manipulated, and interpreted. This article will explore the concept of dimensions in NumPy arrays, often referred to as the shape of the array. We will delve into how to create arrays with different dimensions, how to manipulate these dimensions, and how to apply operations across various dimensions.

1. Introduction to Array Dimensions

In NumPy, dimensions are levels of array depth. For example, a 1D array is a simple list of values, a 2D array is a matrix, and a 3D array can be visualized as a stack of matrices. The number of dimensions is known as the rank of the array.

Example 1: Creating a 1D Array

import numpy as np

# Creating a 1D array
array_1d = np.array([1, 2, 3, 4, 5])
print(array_1d)

Output:

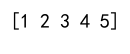
Example 2: Creating a 2D Array

import numpy as np

# Creating a 2D array
array_2d = np.array([[1, 2, 3], [4, 5, 6]])
print(array_2d)

Output:

Example 3: Creating a 3D Array

import numpy as np

# Creating a 3D array
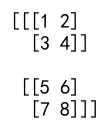
array_3d = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
print(array_3d)

Output:

2. Accessing Array Dimensions

The shape of an array can be accessed using the .shape attribute, which returns a tuple representing the size of the array along each dimension.

Example 4: Accessing the Shape of an Array

import numpy as np

# Creating a 2D array
array_2d = np.array([[1, 2, 3], [4, 5, 6]])
print(array_2d.shape)

Output:

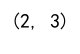
3. Modifying Array Dimensions

You can change the dimensions of an existing array using the reshape method. This is useful for reorganizing data to fit a specific processing requirement.

Example 5: Reshaping an Array

import numpy as np

# Creating and reshaping a 1D array to a 2D array
array_1d = np.array([1, 2, 3, 4, 6, 7, 8, 9])
array_2d = array_1d.reshape(4, 2)
print(array_2d)

Output:

4. Adding Dimensions

Numpy allows you to add new dimensions to an array, enabling you to convert a 1D array into a 2D row or column matrix.

Example 6: Adding a New Dimension

import numpy as np

# Adding a new dimension to create a column matrix
array_1d = np.array([1, 2, 3, 4])
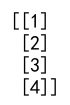
column_matrix = array_1d[:, np.newaxis]
print(column_matrix)

Output:

5. Squeezing and Expanding Dimensions

Sometimes, you may need to remove single-dimensional entries from the shape of an array or add an axis at a specific position.

Example 7: Squeezing an Array

import numpy as np

# Removing single-dimensional entries
array_2d = np.array([[1], [2], [3]])
squeezed_array = np.squeeze(array_2d)
print(squeezed_array)

Output:

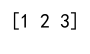
Example 8: Expanding an Array

import numpy as np

# Expanding an array at axis 0
array_1d = np.array([1, 2, 3])
expanded_array = np.expand_dims(array_1d, axis=0)
print(expanded_array)

Output:

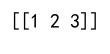
6. Transposing Arrays

Transposing is a common operation in linear algebra where the array’s rows become columns and vice versa.

Example 9: Transposing a 2D Array

import numpy as np

# Transposing a 2D array
array_2d = np.array([[1, 2, 3], [4, 5, 6]])
transposed_array = np.transpose(array_2d)
print(transposed_array)

Output:

7. Broadcasting Across Dimensions

Broadcasting is a powerful mechanism that allows numpy to work with arrays of different shapes when performing arithmetic operations.

Example 10: Broadcasting in Arithmetic Operations

import numpy as np

# Broadcasting a scalar to a 2D array
array_2d = np.array([[1, 2, 3], [4, 5, 6]])
result = array_2d + 10
print(result)

Output:

Numpy Array Dimensions Conclusion

Understanding and manipulating the dimensions of numpy arrays is fundamental for efficient data manipulation and analysis in Python. This article has covered the basics of array dimensions, including creating arrays with different dimensions, accessing, modifying, and manipulating these dimensions, and performing operations across dimensions. With this knowledge, you can effectively manage and analyze large datasets, leveraging the power of numpy to perform complex mathematical operations efficiently.